FFLUX: Force Field Development
Decades of literature evidence show that standard force fields give widely differing answers on the structure and dynamics of proteins. This status-quo harms the relation between simulation and experiment. Remedies usually add or take away often ill-defined energy terms or repeatedly re-parameterise. Unfortunately, this strategy has not led to irreversible progress. This situation urgently calls for a complete overhaul of force field architecture, one that is closer to the underlying quantum reality and that uses a highly transferable atom.
Starting from scratch is a huge undertaking, yet feasible thanks to many proofs-of-concept that we previously obtained. Hence, it is possible to reach the ambitious goal of stabilising protein simulation, delivered by the proposed polarisable, many-body and multipolar force field called FFLUX. In its totality, FFLUX will generate accurate properties for protein systems of the order of tens of thousands of atoms, and over tens of nanoseconds. This system size and time scale suffice to show that FFLUX delivers reliable answers for intrinsically disordered proteins, including those important in Alzheimer’s disease.
FFLUX’s strength is the clarity and minimal character of its design. Its accuracy follows from a precise control over 4 primary energy types, calculated for quantum topological atoms, and from which all chemical phenomena emerge. These energies have a clear chemical interpretation and directly derive from the first- and second-order reduced density matrix, and are accurately learnt by the machine learning method Gaussian Process regression. Our carefully planned work flow is rooted in single amino acids and water clusters, and scaled up via a sequence of test systems, both in gas-phase and aqueous solution. We also implement state-of-art MPI parallellisation on CPUs, GPUs and FPGAs. At any stage, precise validation controls progress thereby guaranteeing genuine advances.
The quantum topological approach divides molecules into atoms in a natural and unbiased way. It generates unique atoms, carved out of their molecular environment. The first three-dimensional pictures of topological atoms were produced in 1994 [13], in a paper that stressed that the topological approach is a departure from the conventional way of defining molecular fragments in the Hilbert space of the basis functions. Because each topological atom is unique there are millions of atoms but transferability enables them to be grouped in atom types by similarity. We have generated a data set of all atoms occurring in one conformation of each natural amino acid and smaller derived molecules. Cluster analysis revealed atom types for carbon [64], hydrogen, nitrogen, oxygen and sulfur [65]. These atom types are constructed in the opposite way to the construction of atom types in force fields. In force field design one starts from a single atom type per atomic number and gradually introduces new types according to the need for accuracy from the force field. We spent much attention to the question how much the integration error influences atomic properties [38]. To our knowledge this is the first time that atom types are being computed rather than postulated. They may guide the design of future force fields [67].
AIBL pKa Prediction
One of the most important and well known physicochemical properties is the acidity constant, usually referred to as pKa and typically measured in (aqueous) solution. Predicting its value remains a challenge, which is addressed worldwide by very few research groups only. This is odd because commercial packages are known to sometimes fail badly or be it in need of further improvement when predictions are reasonable.
Over the last decade our lab perfected its own pKa prediction method, called AIBL, which is remarkably minimal yet powerful. In a way it is curious that this method has been overlooked during the development of the current spectrum of methods, which range from first principle calculations to de facto look-up tables. In fact, we stumbled on AIBL via a detour involving so-called quantum topological descriptors. The latter appear in a QSAR/QSPR approach called Quantum Topological Molecular Similarity (QTMS) (e.g. 1-2) that we developed long before AIBL. In QTMS the so-called bond critical points featured as the positions in a molecule at which various quantum chemical functions were evaluated to provide a “quantum fingerprint”3 of that molecule. The concept of molecular similarity grew even earlier from comparing whole electron densities or later electrostatic potentials. However, we proved that this approach was overkill and that bond critical properties sufficed as much more compact and effective descriptors.
Now, early on, we discovered the existence4 of local linear relationships between bond critical point properties and equilibrium bond lengths, only if the bonds vary little in their chemical surroundings. Such relationships break down completely, however, for larger subsets of bond critical points encompassing a wider variety of bonds. Hence, if one is interested in predicting pKa within a congeneric series of molecules, then bond lengths alone are enough. This realisation led to the birth of AIBL (pronounced “able”), which stands for Ab Initio Bond Length.
AIBL is an empirical-based method (i.e. needing calibration to experimental data), but one that employs quantum mechanically-derived 3D structural information as its descriptors. AIBL works on the basis that for a series of electronic congeners, an equilibrium bond length, typically in the gas phase and close to the site of ionisation, will display a linear relationship with aqueous pKa values. The Figure below illustrates the essence of AIBL in the example context of tautomerisable compounds, a challenging set to predict pKa values for.
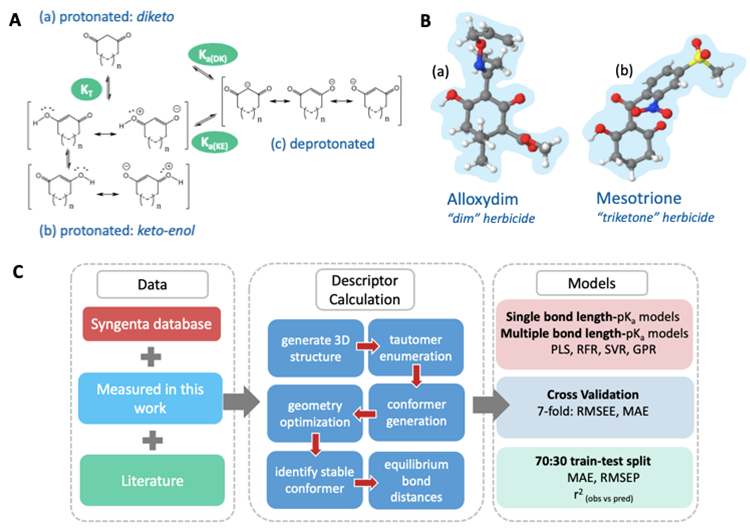
Figure. (a) The diketo form of a 1,3-dione, (b) the resonance canonicals for the keto-enol form of 1,3-diones, and (c) the resonance canonicals for the anionic state, where n=0 or 1 if the ring is five- or six-membered, respectively. KT denotes the equilibrium constant between tautomeric states, Ka(DK) denotes the dissociation equilibrium from the diketo state and Ka(KE) the dissociation equilibrium from the keto-enol state. B. (a) The global minimum geometry of Alloxydim, a 2-oxime herbicide and Mesotrione in the keto-enol anti state, (b) a triketone herbicide. C. The AIBL-pKa workflow implemented here for cyclic -diketones.
Since our original proof-of-concept study on phenols5, we have proven the existence of this simple relationship between solution pKa and equilibrium bond length(s) for a variety of chemistries: benzoic acids6, anilines6, naphthols7, phenylacetic, benzohydroxamic and phenoxyacetic acids8, bicyclo[2,2,2]octane and cubane carboxylic acids9, aryl guanidines and 2-(arylamino)imidazolidines10, guanidines11, guanidine-containing compounds12, sulphonamide drugs13 and tautomerisable herbicides involving 1,3-cyclopentanediones and 1,3-cyclohexanediones14 and other case studies yet to be published, including amidines.
AIBL shows particularly impressive accuracy compared to Marvin, a commercial program by ChemAxon used to predict pKa values for every drug on the online database “DrugBank”: an MAE of 0.20 for a series of 27 2-(arylimino)imidazolidine drugs. The significance of these results is that these compounds contain the guanidine functional group, which is known to be notoriously difficult to predict for. Our work also demonstrates accurate predictions for multiprotic compounds, and most rewardingly, correction of erroneously measured pKa values.
A theoretician’s dream is to truly predict an experimental value. This happened on a number of occasions but most spectacularly while collaborating with Dr Christophe Dardonville in Madrid, Spain, who uses state-of-the-art equipment to measure pKa values. Confident in the predictive capacity of AIBL we told him before his measurement that the answer for the drug Clozapine was 7.76, and teased him in an email asking why one still needed to measure it. Christophe’s returning E-mail stated that the experimental result was 7.77 and that, as a previous non-believer, he was now converted.
The AIBL method has several advantages over other techniques:
(1) Low energy conformations must be identified for 4 species for thermodynamic cycle-based methods, yet AIBL requires only 1, thus vastly reducing computation time. Calculations still take longer than purely empirical methods but there is often a pay-off in terms of increased accuracy.
(2) High levels of theory are required to derive accurate Gibbs energies of the species involved in the pure thermodynamic cycle method. AIBL can work at HF/6-31G(d) but currently B3LYP/6-311G(d,p) is recommended given reasonable timescales.
(3) The relationship between the descriptor and observable is not a “black box”. This means that the occurrence of outliers can usually be explained in a physically meaningful way, i.e. in terms of geometric or chemical similarity.
(4) Multiprotic compounds can be predicted for (proven yet again for sulfonamides and sulfanilamides).
(5) We have developed workflows to form predictive models for tautomerisable compounds including guanidines, amidines, triketones and diketones. We expect this to be applicable to other instances of tautomerisation.
(6) The use of QM-derived 3D structures means that hydrogen bonding and steric effects on pKa are implicitly accounted for, without the need for parameterisation, as in the case for some 2D methods.
(7) Predictions for compounds with ortho-substituents can be problematic due to intramolecular interactions (i.e. hydrogen bonding) with the ipso ionisable group. Our method is capable of making predictions for ortho-compounds by formation of specific predictive equations for subsets of compounds featuring each type of interaction. A meaningful subset can involve just 5 compounds.
In summary, AIBL has proven to be so reliable that if one finds an outlier in its one of its predictions then the only possibilities are that (i) the experiment is wrong and needs to be redone, (ii) an error was made in the bond length calculation, or (iii) the data point belongs to a new subset of congeners that needs to be calibrated. That AIBL would not work is simply not an option… With this happy observation in mind, we hope that researchers will start using AIBL when reliability is important or measurements are inconsistent or missing.
Relative Energy Gradient (REG): Computational Extraction of Chemical Insight from Modern Wavefunctions
There is a universal problem at the heart of chemistry and biochemistry, and it is due to an unbridged gap between chemical insight and quantum mechanics. This problem is best explained by a representative example (see below) but it essentially states that we cannot detect, by computation, which fragment (atoms, functional groups) of a given molecular assembly governs the energetic behaviour of this whole assembly. We call this challenge the fragment rule problem. If we solve it, this quantum based insight will rigorously guide predictions on the relative stability of molecular assemblies.
We propose a general solution to the fragment rule problem, which is the Relative Energy Gradient (REG) method15. This method arms the (bio)chemist with the rigorous capacity to practically transform, for the better, the design of materials, molecular crystals, enzymes and drugs. We put together two methods: the atomistic energy partitioning called Interacting Quantum Atoms (IQA) of Blanco et al.16, and the ranking of atomic energies by their relevance (REG) (see Boxes 1 and 2 below). This combination will revolutionise chemical design in the long term
Box 1: Interacting Quantum Atoms (IQA)
This is the energy partitioning method associated with topological atoms. The intra-atomic energy fits very well to Buckingham potentials and is thus purely steric in nature. The interatomic energies Vee(A,B) are derived from the second-order reduced density-matrix ρ2 and give rise to 3 energy types: electrostatic, exchange and correlation.
Box 2: Relative Energy Gradient (REG) method
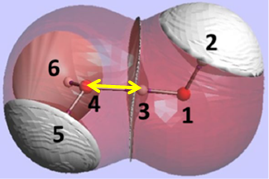
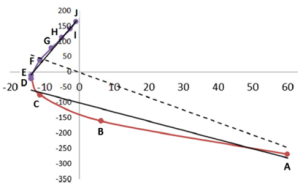
The REG method is dynamic: its control coordinate s (e.g. yellow hydrogen bond length) induces a geometry change in a molecular system (e.g. motion along a reaction coordinate, torsional rotation, here compression of water monomers in a water dimer).
The total energy of the molecular assembly (n atoms) is made up, \[E_{tot}(s) = {\sum_{i=1}^NE_i(s)}\] from N atomic energy contributions Ei, and N=2xn(n-1)/2 + n = n2. The right panel shows that the correlation between Etot and an Ei is best fitted, Ei(s) = mREG,i Etot(s) + ci , in two energy segments: dimer formation, slope mREG is highest (14) of all Ei, i.e. for the electrostatic energy between H3 and O4; for dimer compression the internal steric energy O4 has the highest slope. The Pearson correlations must be | Ri | > 0.95 to be meaningful (dashed line is not but correctly rejects fit over single segment).
In a proof-of-concept case study (Chem. Eur. J. 2018, 24, 11200) on a protease enzyme, REG managed to isolate from a ~130 atoms active site with ~17,000 energy terms, the concerted bond breaking/making mechanism of the substrate’s hydrolysis. REG also identified and quantified O…O through-space interactions with high covalency.
As announced, an example will sharpen the nature of the fragment rule problem. Textbooks state that the guanine…cytosine complex is more stable than the adenine…thymine one because the former is held together by 3 hydrogen bonds while the latter by only 2. In this case, the atoms in the hydrogen bonds constitute the fragment that is supposed to govern the energetic stability of the complexes. Yet, the uracil…2,6-diaminopyridine complex, which also has 3 hydrogen bonds, is two orders of magnitude less stable than guanine…cytosine. Clearly, counting hydrogen bonds does not explain stability. A (bio)chemist wants to understand the behaviour of a system by the presence or action of its relevant atoms. However, this undertaking can derail thereby undermining confidence in chemical intuition.
However, in order to remedy the inadequacy of focusing on hydrogen bonds only, Jorgensen and Pranata proposed17 their secondary interaction hypothesis. This hypothesis is actually a simple rule based on more distant atomic interactions than those involved in the hydrogen bonds only. This rule claims to make reliable predictions of stability, and again on the “back-of-an-envelope”, like hydrogen bonds claim to do. However, this proposal did unfortunately not solve the main problem of how and why a molecular assembly is held together, in terms of key atoms.
Sure, the secondary interaction hypothesis was seized by supramolecular chemists (e.g. Gellman, Zimmerman, Rebek) as the next best concept beyond hydrogen bonding, to explain and predict relative stabilities of various complexes. However, the hypothesis fails18-22 regularly. Furthermore, Popelier and Joubert showed in their paper entitled “the elusive atomic rationale for DNA base pair stability” that Jorgensen’s rule cannot be linked to the underlying quantum reality offered by modern wave functions. In other words, if this rule works on several occasions, it does not do so for the right reasons.
This unsatisfactory state-of-affairs prompts one to look harder to find that much needed, reliable bridge between modern wavefunctions and back-of-an-envelope explanations. This bridge is not just essential for the pivotal example given above but also for a wide variety of recurring questions such as:
- what is the origin of this torsional rotation barrier23?
- what is the degree of covalency24 of this halogen bond?
- which atoms are actually driving this reaction and by which energy type?
- what is the character of these mysterious through-space interactions in this enzyme?
- how is this molecular crystal held together in the curious absence25 of hydrogen bonds?
- why is the distance between these two atoms suspiciously short, again and again? Is there perhaps a new type of non-covalent interaction26 I do not know about?
- if the fluorine gauche-effect is actually electrostatic in nature15 (unlike what Wikipedia claims) then how does this knowledge influence the future design of my compounds in terms of highly desirable conformational control?
With the in-house code REG.py we continue to study and rigorously re-interpret chemical effects and phenomena, the anomeric effect being next in line, to name an example.
References
[1] S. E. O’Brien, P. L. A. Popelier, J.Chem.Inf.Comput.Sci. 2001, 41, 764.
[2] P. L. A. Popelier, P. J. Smith, Eur.J.Med.Chem. 2006, 41, 862.
[3] P. L. A. Popelier, J.Phys.Chem.A 1999, 103, 2883.
[4] S. E. O’Brien, P. L. A. Popelier, Can.J.Chem. 1999, 77, 28.
[5] A. P. Harding, P. L. A. Popelier, Phys.Chem.Chem.Phys. 2011, 13, 11264.
[6] A. P. Harding, P. L. A. Popelier, Phys.Chem.Chem.Phys. 2011, 13, 11283.
[7] C. Anstöter, B. A. Caine, P. L. A. Popelier, J.Chem.Inf.Model. 2016, 56, 471−483.
[8] I. Alkorta, P. L. A. Popelier, ChemPhysChem 2015, 16, 465.
[9] I. Alkorta, M. Z. Griffiths, P. L. A. Popelier, J.Phys.Org.Chem. 2013, 26, 791.
[10] C. Dardonville, B. A. Caine, M. N. de la Fuente, G. M. Herranz, B. C. Mariblanca, P. L. A. Popelier, New J.Chem. 2017, 41, 11016.
[11] M. Z. Griffiths, I. Alkorta, P. L. A. Popelier, Mol.Inf. 2013, 32, 363.
[12] B. A. Caine, C. Dardonville, P. L. A. Popelier, ACS Omega 2018, 3, 3835−3850.
[13] B. A. Caine, M. Bronzato, Paul L. A. Popelier, Chem.Sci. 2019, 10, 6368.
[14] B. A. Caine, M. Bronzato, T. Fraser, N. Kidley, C. Dardonville, P. L. A. Popelier, Comm.Chem. 2020, 3, 21.
[15] J. C. R. Thacker, P. L. A. Popelier, J.Phys.Chem.A 2018, 122, 1439−1450.
[16] M. A. Blanco, A. Martín Pendás, E. Francisco, J.Chem.Theor.Comput. 2005, 1, 1096.
[17] W. L. Jorgensen, J. Pranata, J.Am.Chem. Soc. 1990, 112, 2008.
[18] J. Yang, S. H. Gellman, J.Amer.Chem.Soc. 1998, 120, 9090.
[19] R. R. Gardner, S. H. Gellman, Tetrahedron 1997, 53, 9881.
[20] T. J. Murray, S. C. Zimmerman, J.Am.Chem.Soc. 1992, 114, 4010.
[21] K. S. Jeong, T. Tjivikua, A. Muehldorf, G. Deslongchamps, M. Famulok, J. Rebek, Jr., J.Am.Chem.Soc. 1991, 113, 201.
[22] H. Zeng, R. S. Miller, R. A. Flowers, II, B. Gong, J.Am.Chem.Soc. 2000, 122, 2635.
[23] L. Goodman, V. Pophristic, F. Weinhold, Acc.Chem.Res. 1999, 32, 983.
[24] V. Oliveira, E. Kraka, D. Cremer, Physical Chemistry Chemical Physics 2016, 18, 33031.
[25] R. Paulini, K. Mueller, F. Diederich, Angew.Chemie Int. Ed. 2005, 44, 1788.
[26] I. Alkorta, J. Elguero, A. Frontera, Crystals 2020, 10, 180:1.